Расчет описательных статистик необходим для характеристики «типичного представителя» выборки. Но часто сами цифры мало что могут сказать о выборке и об этом «типично представителе». Чтобы лучше понять полученные данные удобнее воспользоваться визуальным отображением результатов. В данном случае, диаграммой размаха или «ящиком с усами».
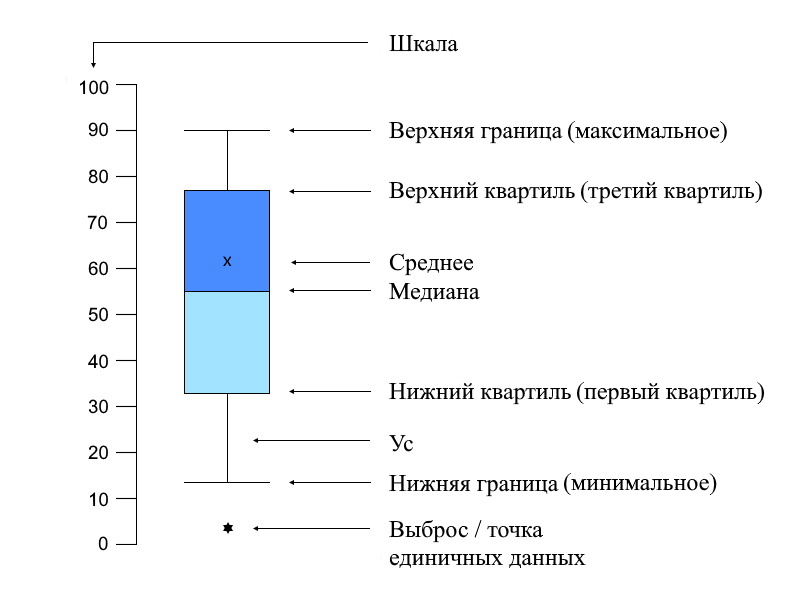
Такая диаграмма в удобной форме показывает медиану, среднее, нижний и верхний квартили, минимальное и максимальное значение выборки и выбросы. Расстояния между различными частями «ящика» позволяют определить степень разброса (дисперсии) и асимметрии данных, а также выявить выбросы.Расположив на одном графике несколько таких «ящиков» можно визуально сравнивать распределение одной переменной с другой.
Чтобы построить такую диаграмму, в первую очередь нам нужно определиться с границами ящика. Ими служат первый и третий квартили (25-й и 75-й процентили соответственно). Линия в середине ящика - это медиана (50-й процентиль). Концы «усов» – это края статистически значимой выборки (без выбросов).
-
Минимальное и максимальное значение данных по выборке (при условии, что мы уверены в отсутствии выбросов).
-
Минимальное значение - это разность первого квартиля (Q1) и полтора межквартильных расстояния (IQR), а максимальное - это сумма третьего квартиля (Q3) и полтора межквартильных расстояния (IQR).
-
Одно стандартное отклонение выше и ниже среднего.
-
9 и 91 процентиль.
-
2 и 98 процентиль.
Любые данные, не попадающие в пространство между «усами», должны быть нанесены на график изолированными точками, малым кругом или звездочками. Но иногда этого не делают. Некоторые «ящики с усами» включают дополнительные символы, чтобы показать среднее значение данных. Иногда, «ящик» может быть представлен вообще без «усов».
В связи с тем, что не существует единого общего мнения относительно того, как конкретно строить «ящик с усами», при виде такого графика необходимо искать информацию в сопроводительном тексте программы относительно того, по каким параметрам он строился.
Если данные имеют нормальное распределение, места расположения обозначений статистических параметров на графике будут равноудаленно распределены.
