Розрахунок описових статистик необхідний для характеристики «типового представника» вибірки. Але часто самі цифри мало що можуть сказати про вибірку та про цього «типового представника». Щоб краще зрозуміти отримані дані зручніше скористатися візуальним відображенням результатів. В даному випадку, діаграмою розмаху або «ящиком з вусами».
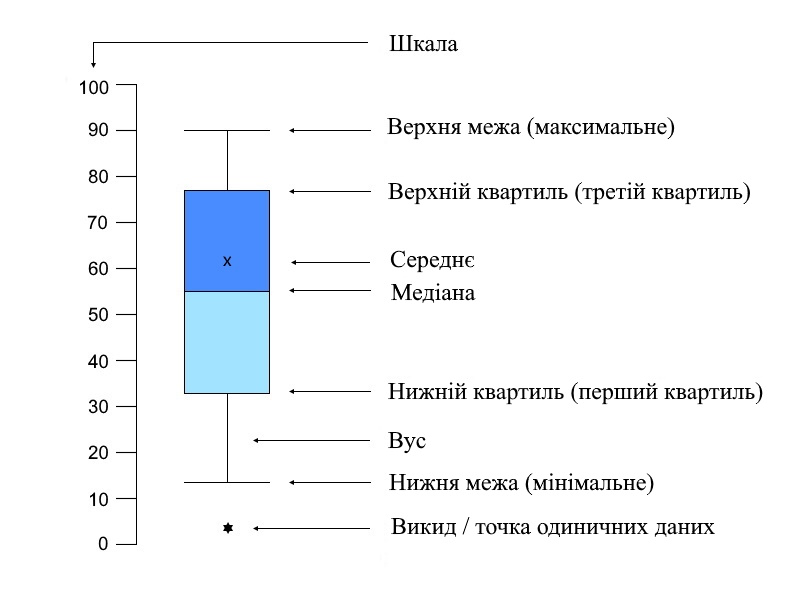
Така діаграма в зручній формі показує медіану, середнє, нижній і верхній квартили, мінімальне і максимальне значення вибірки та викиди. Відстані між різними частинами «ящика» дозволяють визначити ступінь розкиду (дисперсії) і асиметрії даних, а також виявити виброси. Розташувавши на одному графіку кілька таких «ящиків» можна візуально порівнювати розподіл однієї змінної з іншою.
Щоб побудувати таку діаграму, в першу чергу нам потрібно визначитися з межами ящика. Ними служать перший та третій квартили (25-й і 75-й процентилі відповідно). Лінія в середині ящика - це медіана (50-й процентиль). Кінці «вусів» - це краї статистично значущою вибірки (без викидів).
Існує як мінімум п'ять способів визначення довжини «вусів» діаграми.
- Мінімальне і максимальне значення даних за вибіркою (за умови, що ми впевнені у відсутності викидів).
- Мінімальне значення - це різниця першого квартиля (Q1) і півтори міжквартильних відстані (IQR), а максимальне - це сума третього квартиля (Q3) і півтори міжквартильних відстані (IQR).
- Одне стандартне відхилення вище і нижче середнього.
- 9 і 91 процентиль.
- 2 і 98 процентіль.
Будь-які дані, які не потрапляють в простір між «вусами», повинні бути нанесені на графік ізольованими точками, малим колом або зірочками. Але іноді цього не роблять. Деякі «ящики з вусами» включають додаткові символи, щоб показати середнє значення даних. Іноді, «ящик» може бути представлений взагалі без «вусів».
У зв'язку з тим, що не існує єдиної спільної думки щодо того, як саме будувати «ящик з вусами», побачивши такий графік необхідно шукати інформацію в супровідному тексті програми щодо того, за якими параметрами він будувався.
Якщо дані мають нормальний розподіл, місця розташування позначень статистичних параметрів на графіку будуть рівновіддалено розподілені.
