Меры разброса (изменчивости) применяются в психологии для численного выражения величины межиндивидуальной вариации признака и показывают, насколько хорошо данные значения представляют данную совокупность.
Минимальное и максимальное
Минимальное (Xmin) - это наименьшее значение измерения (переменной) в выборке.
Максимальное (Xmax) - это самое большое значение измерения (переменной) в выборке.
Сами по себе эти меры не очень информативны. Особенно если величина распределяется по нормальному закону. Но если мы измеряем какое-то конкретное свойство на примере узкой выборки (например, агрессивность людей, страдающих каким-то заболеванием), то минимальное и максимальное значения могут дать возможность качественно описать эту выборку и лучше понимать особенности ее представителей.
Размах
Размах - разность между наибольшим и наименьшим значениями результатов наблюдений, является одной из самых простых мер изменчивости набора числовых значений. Дает информацию о ширине интервала, в котором сосредоточен весь набор числовых данных, геометрически - ширина отрезка, в котором располагаются все значения.
\( R = X_{max} - X_{min} \)
Простота расчета, наглядность и интуитивная понятность этой характеристики рассеяния значений является очевидным преимуществом перед такими мерами рассеяния как дисперсия и среднее квадратическое отклонение (стандартное отклонение). Существенным недостатком размаха является то, что он не содержит информацию о характере распределения результатов в интервале рассеяния и не устойчив к выбросам, в определенной степени ограничивает его использование.
Пример: допустим у нас есть выборка значений {3,4,5,6,7} где максимальное значение 7, а минимальное 3, получим:
\( R = 7 - 3 = 4 \)
Минимальное, максимальное и размах измерений свойства у представителей двух независимых выборок (например, мужчин и женщин), представленные в виде графика, позволяют визуально определить наличие различий в проявлении изучаемого свойства. А значит предположить влияние признака (в нашем примере –это пол испытуемых) на выраженность свойства.
Межквартильный размах
В статистике для анализа выборки часто прибегают к более стабильному к выбросам показателю вариации – межквартильному размаху (IQR). Квартиль (Q) – это то значение, которое делит отсортированные (ранжированные) данные на части, кратные одной четверти, или 25%, что равносильно 25-му процентлю или квантилю 0.25. Так, 1-й квартиль (Q1) – это значение, ниже которого находится 25% выборки. 2-й квартиль (Q2) делит выборку данных пополам и равен медиане, ну и 3-й квартиль (Q3) это значение выше которого находится 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями.
\( IQR = Q3 -Q1 \)
У данного показателя есть одно неоспоримое преимущество: он является робастным.
Пример: допустим у нас есть выборка отсортированных значений {0,1,3,4,5,6,7,100}. Первым делом определяем медиану по которую выборку разделим на две равные части. Медиана у нас 4.5, получаем две выборки {0,1,3,4} и {5,6,7,100}. Теперь для полученых выборок определим медиану. Для первой это будет 2 и это значение будет соответствовать первому квартилю (Q1). Для второй выборки это будет 6.5 и соответствовать третьему квартилю (Q3). Тогда:
\( IQR = 6.5 - 2 = 4.5 \)
Дисперсия
Один из способов измерения рассеяния данных заключается в том, чтобы определить степень отклонения каждого наблюдения от выборочного среднего. Очевидно, что чем больше отклонение, тем больше изменчивость, вариабельность наблюдений.
Однако мы не можем использовать среднее этих отклонений как меру рассеяния, потому что положительные отклонения компенсируют отрицательные отклонения, их сумма равна нулю. Чтобы решить эту проблему, мы возводим в квадрат каждое отклонение и находим среднее возведенных в квадрат отклонений.
\( D = \sigma^{2}=\frac{\sum_{i=1}^n(X_{i}- \bar{X})^{2}}{n-1} \)
Дисперсия является одним из параметров нормального закона распределения. Чем больше дисперсия, тем более пологими являются "склоны" распределения и длиннее его "хвосты".
Чем выше дисперсия показателей измеряемого свойства (коэффициентов регрессии, значений переменных и т.д.), тем менее устойчивой она будет. Высокая дисперсия исходных данных позволяет предположить высокую значимость в них случайной компоненты, возможном наличии шума, выбросов и аномальных значений.
Пример: допустим у нас есть выборка значений {3,4,5,6,7} первым делом расчитываем выборочное среднее:
\( \bar{X}=\frac{3+4+5+6+7}{5}=\frac{25}{5}=5 \)
Теперь приступим к расчету дисперсии
\( D=\frac{(3-5)^{2}+(4-5)^{2}+(5-5)^{2}+(6-5)^{2}+(7-5)^{2}}{5-1} = \frac{4+1+0+1+4}{4} = 2.5 \)
К сожалению, не существует никаких ориентиров, чтобы интерпретировать величину дисперсии. Тем более, что на ее величину будет влиять размер шкалы измерения. Однако, расчет дисперсии нам необходим для определения следующих статистик.
Стандартное отклонение
Это наиболее распространенный показатель в статистике и теории вероятности, оценивающий среднеквадратичное отклонение случайной величины относительно ее математического ожидания на основе несмещенной оценки ее дисперсии. Измеряется в единицах измерения самой случайной величины.
\( \sigma=\sqrt{D}=\sqrt{\frac{\sum_{i=1}^n(X_{i}- \bar{X})^{2}}{n-1}} \)
Если перейти на "человеческий" язык, то стандартное отклонение - это показатель того, насколько резво какой-либо показатель меняется со временем или у разных людей. Т.е. чем больше этот показатель, тем сильнее изменчивость ряда значений.
Стандартное отклонение используют для анализа наборов значений. Иногда два набора с одинаковым средним значением могут оказаться совершенно разными по разбросу величин.
Пример: расчитывать стандартное отклонение достаточное легко после того как расчитали дисперсию. Допустим у нас есть все та же выборка {3,4,5,6,7}, для нее мы уже расчитали дисперсию и она равна 2.5, тогда
\( \sigma=\sqrt{2.5} = 1.58113883 \)
Синонимы:
- среднее квадратическое отклонение
- среднеквадратичное отклонение
- среднеквадратическое отклонение
- квадратичное отклонение
- стандартный разброс
Для психологии расчет стандартного отклонения необходим для определения нормативных интервалов выраженности свойства. Для этого используется «правило трех сигм».
Это правило утверждает, что вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три среднеквадратических отклонения, практически равна нулю. Правило справедливо только для случайных величин, распределенных по нормальному закону, поэтому часто используется в современной психометрике.
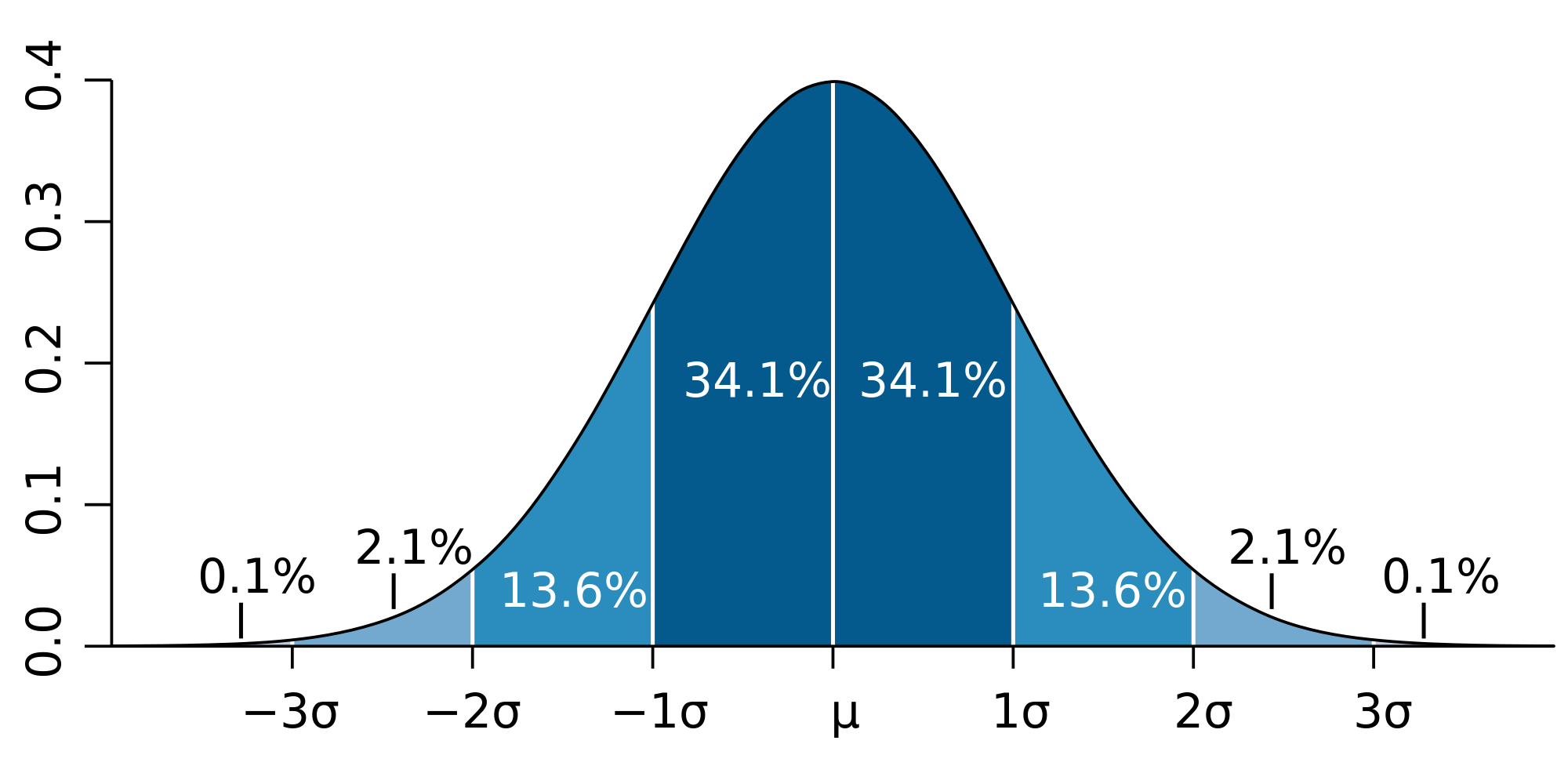
Как показано на рисунке интервал [-3σ;-1σ] – это значения, соответствующие низкому уровню выраженности свойства, интервал[-1σ;1σ] – среднему уровню, а интервал [1σ;3σ] – высокому.
Коэффициент вариации
Коэффициент вариации - это величина, используемая в статистике, равная отношению стандартного отклонения случайной величины к ее математическому ожиданию (среднему выборочному). Он применяется для сравнения вариативности одного и того же признака в нескольких совокупностях с различным средним арифметическим. Т.к. коэффициент вариации величина относительная, то обычно она выржаеться в процентах.
\( CV = \frac{\sigma}{\bar{X}}\cdot100 \)
В статистике принято, что:
- если коэффициент вариации меньше 10%, то степень рассеивания данных считается незначительной;
- если от 10% до 20% - средней;
- больше 20% и меньше или равно 33% - значительной.
Если значение коэффициента вариации не превышает 33%, то совокупность считается однородной, а если больше 33%, то - неоднородной.
Пример: берем ранее используемый ряд данных {3,4,5,6,7}, для него у нас посчитано уже и стандартное отклонение и выборочное среднее, получим:
\( CV = \frac{1.58113883}{5}\cdot100 = 31.6227766 \)
Исходя из получившегося результата можем утверждать, что степень рассеивания данных значительная, а сама выборка однородная. Если бы мы изучали какое-то свойство, это бы означало, что оно стабильно закрепилось у представителей выборки на уровне, соответствующем среднему выборочному. А значит мы можем смело утверждать, что изучаемое свойство характерно для представителей нашей выборки.
Если после прочтения этой статьи вы почувствовали, что какие-то мысли задели вас особенно сильно — это нормально. Иногда одна фраза может напомнить о том, что мы долго прятали внутри. Такие моменты — хороший повод остановиться и прислушаться к себе. И если вы чувствуете, что хочется поговорить, разобраться в себе, получить поддержку — не откладывайте это надолго. На нашем сайте вы всегда можете обратиться за помощью к психологу онлайн.


