Міри розкиду (мінливості) застосовуються в психології для чисельного вираження величини міжіндивідуальної варіації ознаки і показують, наскільки добре ці значення представляють дану сукупність.
Мінімальне та максимальне
Мінімальне (Xmin) - це найменше значення вимірювання (змінної) у вибірці.
Максимальне (Xmax) - це найбільше значення вимірювання (змінної) у вибірці.
Самі по собі ці заходи не дуже інформативні. Особливо якщо величина розподіляється за нормальним законом. Але якщо ми вимірюємо якусь конкретну властивість на прикладі вузької вибірки (наприклад, агресивність людей, які страждають якимось захворюванням), то мінімальне і максимальне значення можуть дати можливість якісно описати цю вибірку і краще розуміти особливості її представників.
Розмах
Розмах - різниця між найбільшим і найменшим значеннями результатів спостережень, є однією з найпростіших мір мінливості набору числових значень. Дає інформацію про ширину інтервалу, в якому зосереджений весь набір числових даних, геометрично - ширина відрізка, в якому розташовуються всі значення.
\( R = X_{max} - X_{min} \)
Простота розрахунку, наочність та інтуїтивна зрозумілість цієї характеристики розсіювання значень є очевидною перевагою перед такими мірами розсіювання як дисперсія чи середнє квадратичне відхилення (стандартне відхилення). Істотним недоліком розмаху є те, що він не містить інформацію про характер розподілу результатів в інтервалі розсіювання та є не стійким до викидів, певною мірою обмежує його використання.
Приклад: припустимо у нас є вибірка значень {3,4,5,6,7} де максимальне значення 7, а мінімальне 3, отримаємо:
\( R = 7 - 3 = 4 \)
Мінімальне, максимальне і розмах вимірювань властивості у представників двох незалежних вибірок (наприклад, чоловіків та жінок), представлені у вигляді графіка, дозволяють візуально визначити наявність відмінностей в прояві досліджуваної властивості. А отже припустити вплив ознаки (в нашому прикладі це стать випробовуваних) на вираженість властивості.
Міжквартільний розмах
У статистиці для аналізу вибірки часто вдаються до більш стабільного до викидів показнику варіації - міжквартільного розмаху (IQR). Квартиль (Q) - це таке значення, що ділить відсортовані (ранжируванні) дані на частини, кратні одній чверті, або 25%, що відповідає 25-му процентлю або квантилю 0.25. Так, 1-й квартиль (Q1) - це значення, нижче якого знаходиться 25% вибірки. 2-й квартиль (Q2) ділить вибірку даних навпіл і дорівнює медіані, ну і 3-й квартиль (Q3) це значення вище якого знаходиться 25% максимальних значень. Так ось міжквартільний розмах - це різниця між 3-м і 1-м квартилями.
\( IQR = Q3 -Q1 \)
У цього показника є одна незаперечна перевага: він є робастним.
Приклад: припустимо у нас є вибірка відсортованих значень {0,1,3,4,5,6,7,100}. Насамперед визначаємо медіану за якою вибірку розділимо на дві рівні частини. Медіана у нас 4.5, отримуємо дві вибірки {0,1,3,4} і {5,6,7,100}. Тепер для отриманих вибірок визначимо медіану. Для першої це буде 2 і це значення буде відповідати першому квартилю (Q1). Для другої вибірки це буде 6.5 і відповідати третьому квартилю (Q3). Тоді:
\( IQR = 6.5 - 2 = 4.5 \)
Дисперсія
Один із способів вимірювання розсіювання даних полягає в тому, щоб визначити ступінь відхилення кожного спостереження від вибіркового середнього. Очевидно, що чим більше відхилення, тим більше мінливість, варіабельність спостережень.
Однак ми не можемо використовувати середнє цих відхилень як міру розсіювання, тому що позитивні відхилення компенсують негативні відхилення, їх сума дорівнює нулю. Щоб вирішити цю проблему, ми підносимо у квадрат кожне відхилення і знаходимо середнє піднесених в квадрат відхилень.
\( D = \sigma^{2}=\frac{\sum_{i=1}^n(X_{i}- \bar{X})^{2}}{n-1} \)
Дисперсія є одним з параметрів нормального закону розподілу. Чим більше дисперсія, тим більш пологими є "схили" розподілу і довше його "хвости".
Чим вищою є дисперсія показників вимірюваної властивості (коефіцієнтів регресії, значень змінних тощо.), тим менш стійкою вона буде. Висока дисперсія вихідних даних дозволяє припустити високу значущість в них випадкової компоненти, можливу наявність шуму, викидів та аномальних значень.
Приклад: припустимо у нас є вибірка значень {3,4,5,6,7} насамперед розраховуємо вибіркове середнє:
\( \bar{X}=\frac{3+4+5+6+7}{5}=\frac{25}{5}=5 \)
Тепер приступимо до розрахунку дисперсії.
\( D=\frac{(3-5)^{2}+(4-5)^{2}+(5-5)^{2}+(6-5)^{2}+(7-5)^{2}}{5-1} = \frac{4+1+0+1+4}{4} = 2.5 \)
На жаль, не існує ніяких орієнтирів, щоб інтерпретувати величину дисперсії. Тим більше, що на її величину буде впливати розмір шкали вимірювання. Однак, розрахунок дисперсії нам необхідний для визначення наступних статистик.
Стандартне відхилення
Це найбільш поширений показник в статистиці і теорії ймовірності, що оцінює середньоквадратичне відхилення випадкової величини щодо її математичного очікування на основі незміщеної оцінки її дисперсії. Вимірюється в одиницях виміру самої випадкової величини.
\( \sigma=\sqrt{D}=\sqrt{\frac{\sum_{i=1}^n(X_{i}- \bar{X})^{2}}{n-1}} \)
Якщо перейти на "людську" мову, то стандартне відхилення - це показник того, наскільки жваво будь-який показник змінюється з часом або у різних людей. Тобто чим більше цей показник, тим сильніше мінливість ряду значень.
Стандартне відхилення використовують для аналізу наборів значень. Іноді два набори з однаковим середнім значенням можуть виявитися зовсім різними за розкидом величин.
Приклад: розраховувати стандартне відхилення достатню легко після того як розрахували дисперсію. Припустимо у нас є та сама вибірка {3,4,5,6,7}, для неї ми вже розрахували дисперсію і вона дорівнює 2.5, тоді:
\( \sigma=\sqrt{2.5} = 1.58113883 \)
Синоніми:
- середнє квадратичне відхилення
- середньоквадратичне відхилення
- квадратичне відхилення
- стандартний розкид
Для психології розрахунок стандартного відхилення необхідний для визначення нормативних інтервалів вираженості властивості. Для цього використовується «правило трьох сигм».
Це правило стверджує, що ймовірність того, що випадкова величина відхилиться від свого математичного очікування більш ніж на три середньоквадратичних відхилення, практично дорівнює нулю. Правило є справедливим тільки для випадкових величин, розподілених за нормальним законом, тому часто використовується в сучасній псіхометриці.
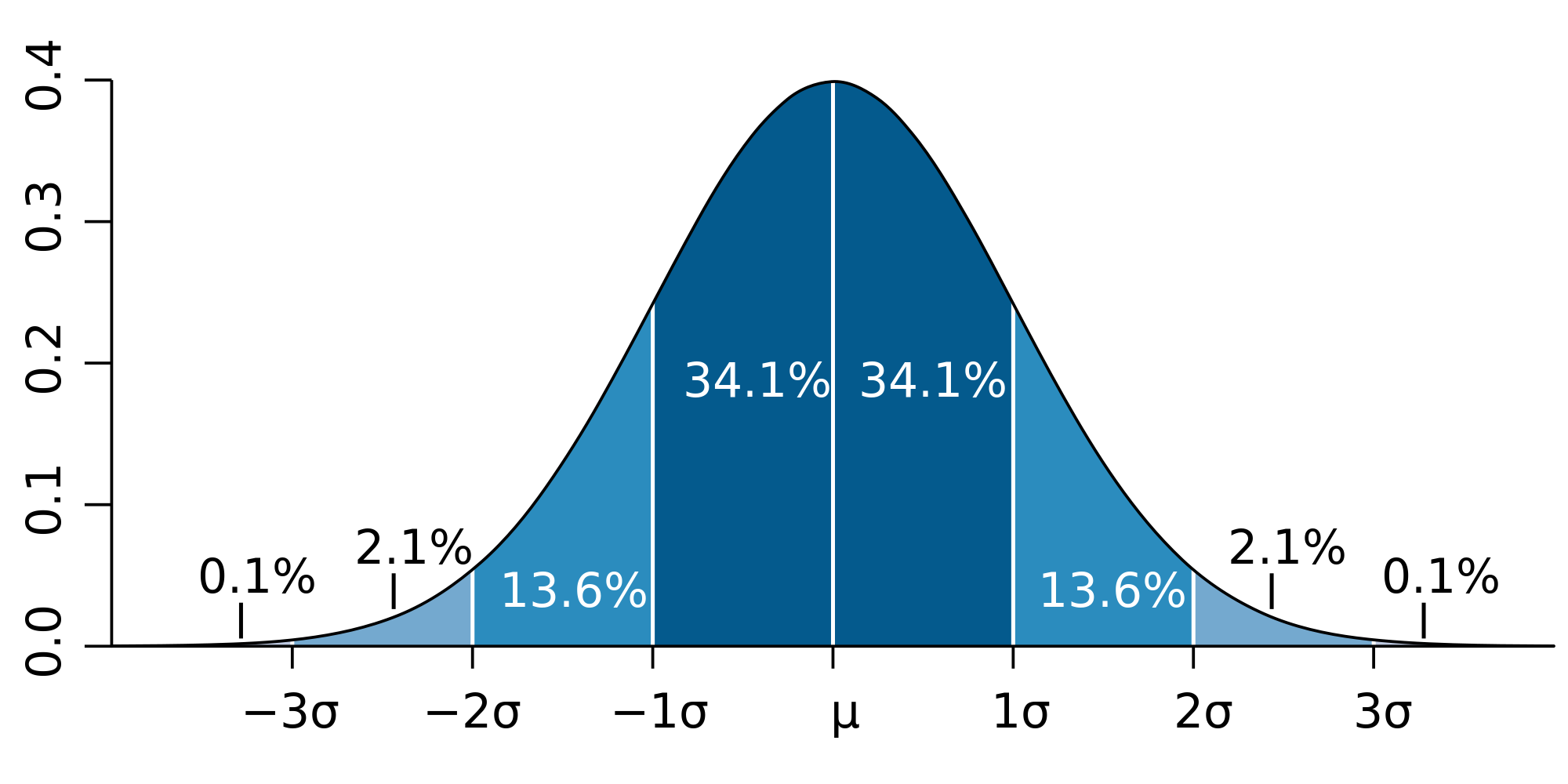
Як показано на малюнку інтервал [-3σ; -1σ] - це значення, які відповідають низькому рівню вираженості властивості, інтервал [-1σ; 1σ] - середньому рівню, а інтервал [1σ; 3σ] - високому.
Приклад:
Ми вимірюємо швидкість мислення за шкалою від 0 до 12. Для застосування правила нам потрібно вирахувати середнє вибіркове і стандартне відхилення.
Припустимо, ми визначили, що середнє М = 7, а стандартне відхилення σ = 1,5.
Далі, як показано на малюнку, нам потрібно тричі відняти стандартне відхилення від середнього (отримаємо: -1σ = 5,5; -2σ = 4, -3σ = 2,5), і тричі додати (1σ = 8,5; 2σ = 10, 3σ = 11,5).
Таким чином отримаємо інтервал низьких значень [2,5; 5,5]; інтервал середніх значень [5,5; 8,5]; інтервал високих значень [8,5; 11,5].
Коефіцієнт варіації
Коефіцієнт варіації - це величина, яка використовується в статистиці, що дорівнює відношенню стандартного відхилення випадкової величини до її математичного сподівання (середнього вибіркового). Він застосовується для порівняння варіативності однієї і тієї ж ознаки в декількох сукупностях з різним середнім арифметичним. Оскільки коефіцієнт варіації величина відносна, то зазвичай вона виржаеться в процентах.
\( CV = \frac{\sigma}{\bar{X}}\cdot100 \)
У статистиці заведено, що:
- якщо коефіцієнт варіації менше 10%, то ступінь розсіювання даних вважається незначною;
- якщо від 10% до 20% - середньої;
- більше 20% і менше або дорівнює 33% - значною.
Якщо значення коефіцієнта варіації не перевищує 33%, то сукупність вважається однорідною, а якщо більше 33%, то - неоднорідною.
Приклад: беремо раніше використовуваний ряд даних {3,4,5,6,7}, для нього у нас пораховано вже і стандартне відхилення і вибіркове середнє, отримаємо:
\( CV = \frac{1.58113883}{5}\cdot100 = 31.6227766 \)
Виходячи з отриманого результату можемо стверджувати, що ступінь розсіювання даних значна, а сама вибірка однорідна. Якби ми вивчали якусь властивість, це б означало, що вона стабільно закріпилася у представників вибірки на рівні, який відповідає середньому вибірковому. А значить ми можемо сміливо стверджувати, що досліджувана властивість є характерною для представників нашої вибірки.
